a) Dibujar la región del plano que definen, y calcular sus vértices.
b) Hallar el punto de esa región en el que la función F(x,y) = 6x + 4y alcanza el valor máximo y calcular dicho valor.
| Actividades resueltas |
1) Se considera la región del plano
determinada por las inecuaciones:x
+ 3 ![]() y ; 8
y ; 8 ![]() x + y ;
y
x + y ;
y ![]() x
- 3 ; x
x
- 3 ; x ![]() 0; y
0; y
![]() 0
0
a) Dibujar la región del plano que definen, y calcular sus
vértices.
b) Hallar el punto de esa región en el que la función F(x,y)
= 6x + 4y
alcanza el valor máximo y calcular dicho
valor.
a ) Hay que dibujar la región factible correspondiente. Para ello vamos a representar las rectas:
x - y = - 3 ; x + y = 8 ; x - y = 3
La región factible es la determinada por los vértices O, A, B, C y D.
Las coordenadas de los vértices son: A(3,0) ; B(5.5, 2.5) ; C(2.5, 5.5) ; D(0,3) y O(0,0)
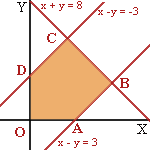
b) Para determinar dónde la función objetivo F(x,y) = 6x + 4y alcanza su máximo, calculamos los valores que toma en los vértices:
F(A) = 18 ; F(B) = 43 ; F(C) = 37 ; F(D) = 12 ; F(O) = 0.
Luego la función alcanza su máximo en el vértice B y su valor es 43.
2)![]() Las restricciones pesqueras
impuestas por la CEE obligan a cierta empresa a pescar como
máximo 2.000 toneladas de merluza y 2.000 toneladas de rape,
además, en total, las capturas de estas dos especies no pueden
pasar de las 3.000 toneladas. Si el precio de la merluza es de
1.000 ptas/kg y el precio del rape es de 1.500 ptas/kg, ¿qué
cantidades debe pescar para obtener el máximo beneficio?
Las restricciones pesqueras
impuestas por la CEE obligan a cierta empresa a pescar como
máximo 2.000 toneladas de merluza y 2.000 toneladas de rape,
además, en total, las capturas de estas dos especies no pueden
pasar de las 3.000 toneladas. Si el precio de la merluza es de
1.000 ptas/kg y el precio del rape es de 1.500 ptas/kg, ¿qué
cantidades debe pescar para obtener el máximo beneficio?
Sean :
x = número de toneladas de merluza
y = número de toneladas de rape
Del enunciado deducimos las restricciones:
La función objetivo que da el
beneficio en miles de pesetas y que hay que maximizar viene dada
por:
f(x,y) = 1000x + 1500y
Representando las rectas: x = 2000, y = 2000 , x + y = 3000 correspondientes a las fronteras de las restricciones obtenemos la región factible:
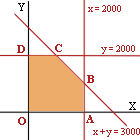
Donde los vértices
obtenidos son:
A(2000,0) ; B(2000, 1000) ; C(1000, 2000) , D(0,2000) y O(0,0)
Al sustituir sus coordenadas en la función objetivo f resulta :
f(A) = 2000 millones de ptas. ; f(B) = 3500 millones de pesetas; f(C) = 4000 millones de pesetas ; f(D) = 3000 millones de pesetas y f(O)= 0 ptas.
La función objetivo alcanza su máximo en el vértice C, por lo que las cantidades a pescar son 1000 toneladas de merluza y 2000 toneladas de rape.
3) Dos pinturas A y B tienen ambas dos
tipos de pigmentos p y q; A está compuesto de un 30% de p y un
40% de q, B está compuesto de un 50% de p y un 20% de q, siendo
el resto incoloro. Se mezclan A y B con las siguientes
restricciones:
La cantidad de A es mayor que la de B. Su diferencia no es menor
que 10 gramos y no supera los 30 gramos. B no puede superar los
30 gramos ni ser inferior a 10 gramos.
Sean x e y, respectivamente, los gramos de las pinturas A y B que aparecen en la mezcla. Traduzcamos a inecuaciones las restricciones a las que se han de someter esas cantidades.
Además sabemos que : x ![]() 0 , y
0 , y ![]() 0.
0.
Veamos las cantidades de pigmento de cada tipo:
Cantidad de pigmento de tipo p: Fp
(x, y) = 0.3x + 0.5y
Cantidad de pigmento de tipo q: Fq (x, y) =
0.4x + 0.2y
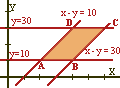 La
región factible es la que aparece en la imagen del margen.
La
región factible es la que aparece en la imagen del margen.
Sus vértices son A(20,10) , B(40,10), C(60,30) y D(40,30)
a) La mayor cantidad de pigmento
p, se produce para 60 gramos de la pintura A y 30 de la B:
Fp (40,30) = 0.3·40 + 0.5·30 = 27 ; Fp (20,10)
= 11 ; Fp (40, 10) = 17; Fp (60, 30) = 33
b) La menor cantidad de pigmento
q, se produce para 20 gramos de la pintura A y 10 de la B:
Fq (40, 30) = 0.4·40 + 0.2·30 = 22; Fq (20,
10) = 10 ; Fq (40, 10) = 18 ; Fq (60, 30) =
30
| 4) Problema del transporte | |||||||||||||||
| Una empresa dedicada a la fabricación de componentes de ordenador tiene dos fábricas que producen, respectivamente, 800 y 1500 piezas mensuales. Estas piezas han de ser transportadas a tres tiendas que necesitan 1000, 700 y 600 piezas, respectivamente. Los costes de transporte, en pesetas por pieza son los que aparecen en la tabla adjunta. ¿Cómo debe organizarse el transporte para que el coste sea mínimo? | Un problema particular que
se resuelve con los procedimientos de la programación
lineal es la situación conocida como problema del
transporte o problema de la distribución de mercancías. Se trata de encontrar los caminos para trasladar mercancía, desde varias plantas (orígenes) a diferentes centros de almacenamiento (destinos), de manera que se minimice el costo del transporte. |
||||||||||||||
|
Para que un problema pueda ser
resuelto por el método del transporte debe cumplir:
|
En este tipo de problemas se exige que toda la producción sea distribuida a los centros de ventas en las cantidades que precisa cada uno; por tanto, no pueden generarse stocks del producto ni en las fábricas ni en los centros de ventas.
En consecuencia, los 800
artículos producidos en la fábrica I deben distribuirse en las
cantidades x, y, z a A, B y C, de manera que x + y +
z = 800. Pero, además, si desde I se envían x
unidades a A, el resto, hasta las 1000 necesarias en A, deben ser
enviadas desde la fábrica II; esto es, 1000 - x unidades
serán enviadas desde II a A.
Del mismo modo, si desde I a B se envían y, el resto
necesario, 700 - y, deben enviarse desde II. Y lo mismo
para C, que recibirá z desde I y 600 - z desde
II.
En la siguiente tabla de distribución se resume lo dicho:
| Envíos | a la tienda A (1000) | a la tienda B (700) | a la tienda C (600) |
| Desde la fábrica I ( 800) | x | y | 800 - x - y |
| Desde la fábrica II (1500) | 1000 - x | 700 - y | x + y - 200 |
La última columna la hemos
obtenido de la siguiente forma:
Como x + y + z = 800 , se tiene que z = 800 - x
- y, de donde, 600 - z = 600 - (800 - x - y)
= x + y - 200.
Ahora bien, todas las cantidades anteriores deben ser mayores o iguales que cero. Por tanto, se obtienen las siguientes desigualdades:
x ![]() 0 ; 1000 - x
0 ; 1000 - x ![]() 0 ; y
0 ; y ![]() 0; 700 - y
0; 700 - y ![]() 0 ; 800 - x - y
0 ; 800 - x - y ![]() 0 ; x + y - 200
0 ; x + y - 200 ![]() 0
0
Simplificando las desigualdades anteriores, se obtienen las siguientes inecuaciones:
1000 ![]() x
x ![]() 0 ; 700
0 ; 700 ![]() y
y ![]() 0 ; 800
0 ; 800 ![]() x + y
x + y ![]() 0
0
Recordemos que
nuestro objetivo es abaratar al máximo los costes de transporte.
Estos costes se hallan multiplicando las cantidades enviadas a
desde cada fábrica a cada tienda por los respectivos costes de
transporte unitario.
Se obtiene:
Z = f(x,y) = 3x + 2(1000 - x) + 7y + 2(700 - y) + (800 - x - y) + 6(x + y - 200) = 6x + 10y + 3000
En definitiva, el programa lineal a resolver es :
| Minimizar: | Z = 6x + 10y + 3000 |
| sujeto a: | 1000 |
| 700 |
|
| 800 |
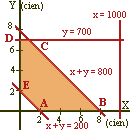 La región factible se
da en la imagen del margen.
La región factible se
da en la imagen del margen.
Sus vértices son A(200,0) ; B(800,0) ; C(100,700) ; D(0,700) y E(0,200).
El coste, el valor de Z en cada uno de esos puntos, es:
El mínimo se da en A , cuando x = 200 e y = 0.
Luego, las cantidades a distribuir son:
| Envíos | a la tienda A (1000) | a la tienda B (700) | a la tienda C (600) |
| Desde la fábrica I ( 800) | 200 | 0 | 600 |
| Desde la fábrica II (1500) | 800 | 700 | 0 |
| 5) Problema de la dieta | |
| En
una granja de pollos se da una dieta "para
engordar" con una composición mínima de 15
unidades de una sustancia A y otras 15 de una sustancia
B. En el mercado sólo se encuentran dos clases de
compuestos: el tipo X con una composición de una unidad
de A y cinco de B, y el tipo Y, con una composición de
cinco unidades de A y una de B. El precio del tipo X es
de 1000 pesetas y el del tipo Y es de 3000 pesetas. Se
pregunta: ¿Qué cantidades se han de comprar de cada tipo para cubrir las necesidades con un coste mínimo ? (Islas Baleares. Junio 1990) |
El problema se llama así
porque en sus orígenes consistió únicamente en
determinar la dieta humana más económica. En su forma industrial más corriente, el problema consiste en saber cómo mezclar de la forma más económica posible las materias primas que constituyen un producto de fórmula química conocida. |
Podemos organizar la información mediante una tabla:
| Unidades | Sustancia A | Sustancia B | Coste | |
| Compuesto X | x | x | 5x | 1000x |
| Compuesto Y | y | 5y | y | 3000y |
| Total | 1000x + 3000y |
La función objetivo del coste total, f, si se emplean x kg del compuesto X e y kg del compuesto Y, es :
Z = f(x,y) = 1000x + 3000y
 El
conjunto de restricciones es: x
El
conjunto de restricciones es: x ![]() 0 , y
0 , y ![]() 0 ; x + 5y
0 ; x + 5y ![]() 15 ; 5x + y
15 ; 5x + y ![]() 15 .
15 .
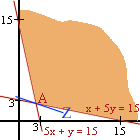
Con estos datos representamos la región factible y las rectas de nivel de la función objetivo.
De todas las rectas de nivel que tocan a la región factible, hace que el coste Z sea mínimo la que pasa por el vértice A(2.5,2.5).
La solución óptima se obtiene comprando 2.5 unidades de X y 2.5 unidades de Y.
El coste total es : Z = f(2.5,2.5) = 1000·2.5 + 3000·2.5 = 10000 pesetas.
6) 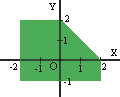 Considera el recinto de la figura
en el que están incluidos todos los lados y todos los vértices.
Considera el recinto de la figura
en el que están incluidos todos los lados y todos los vértices.
a) Escribe la inecuaciones que lo definen
b) Maximiza la función Z = x + y
a)
| (0,2) |
||
| y = mx + n | ||
| (2,0) |
Los puntos del recinto (por
ejemplo, el (0,0) ) verifican x + y ![]() 2
2
Las inecuaciones que cumplen los puntos del recinto son:
| x + y |
| - 2 |
| - 1 |
b) Como la dirección de la
función Z = x + y a maximizar es la misma que la del
borde x + y = 2, resulta que esta recta es tal que deja
todo el recinto a un lado, precisamente del lado que hace x + y ![]() 2 . Por tanto, el máximo de Z = x + y
para (x,y) en el recinto se alcanza para cualquier punto
de ese segmento del borde y tiene por valor 2.
2 . Por tanto, el máximo de Z = x + y
para (x,y) en el recinto se alcanza para cualquier punto
de ese segmento del borde y tiene por valor 2.