ax
+ by = k| Método gráfico |
| o Método de las rectas de nivel |
Las rectas de nivel dan los puntos del plano en los que la función objetivo toma el mismo valor.
Si la función objetivo es f(x,y) = ax + by + c, la ecuación de las rectas de nivel es de la forma:
ax + by
+ c = 0 ax
+ by = k
Variando k (o p) se obtienen distintos niveles para esas rectas y, en consecuencia, distintos valores para f(x,y).
En un problema todas las rectas de nivel son paralelas, pues los coeficientes a y b de la recta ax + by = k son los que determinan su pendiente. Por tanto, si k1 es distinto de k2 , las rectas ax + by = k1 y ax + by = k2 son paralelas. Luego, trazada una cualquiera de esas rectas, las demás de obtienen por desplazamientos paralelos a ella.
Si lo que se pretende es resolver un problema de programación lineal, los únicos puntos que interesan son los de la región factible, y las únicas rectas de nivel que importan son aquellas que están en contacto con dicha región. Como el nivel aumenta (o disminuye) desplazando las rectas, el máximo (o el mínimo) de f(x,y) se alcanzará en el último (o en el primer) punto de contacto de esas rectas con la región factible.
Veamos ahora como se aplica todo esto a la resolución de un problema de programación lineal :
| Maximizar | Z = f(x,y) = x + y |
| sujeto a: | 0  x 4 |
| 0 y 4 |
|
y  x /2 |
1) Representamos la región factible:
x 4 son los puntos entre el eje Y y la recta x
= 4
y 4 son los puntos entre el eje X y la recta y
= 4
x /2 son los puntos de su
izquierda.
Resolviendo los sistemas correspondientes calculamos los vértices de la región factible:
{ y = x/2 , x
= 0 } nos da el vértice O(0,0)
{ x = 4, y = x/2 } nos da el vértice A(4,2)
{ x = 4 , y = 4} nos da el vértice B(4,4)
{ y = 4 , x = 0 } nos da el vértice C(0,4)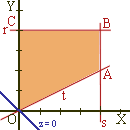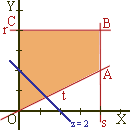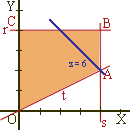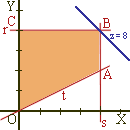
2) Representamos las rectas de nivel :
En nuestro caso son rectas de la forma x + y = k . Inicialmente representamos Z = x + y = 0 . Trasladándola hacia la derecha, obtenemos las rectas : x + y = 2, x + y = 4, x + y = 8 , es decir aumenta el nivel.
3) Obtenemos la solución óptima:
Se obtiene en el punto de la región factible que hace máximo k. En nuestro caso esto ocurre en el punto B; es el último punto de contacto de esas rectas con la región factible , para el que k = 8.
| Si hay dos vértices, P y Q, que se encuentran en la misma recta de nivel ,de ecuación ax + by = k .Es evidente que todos los puntos del segmento PQ son de esa recta; por tanto, en todos ellos f(x,y) vale k. Así pues, la solución óptima es cualquier punto de esa recta; en particular los vértices P y Q. |
