Extracto
de la página http://www.xtec.es/~bfiguera/curioso.html#quadrat
Autor: Blai Figueras Álvarez
NÚMEROS AL CUADRADO
Distancia entre números
al cuadrado
"La
distancia o diferencia entre 2 números consecutivos al cuadrado es la suma de
ambos".
Ejemplos:
8² = 64, mientras que 9² = 81. Su diferencia 81 - 64 = 17, es
decir, 9 + 8 = 17
Esto
es válido en todos los casos... 24² = 576,
25² = 625, la diferencia es 49 = 24 + 25
A partir de aquí podemos definir que la distancia entre 2 números
cualquiera al cuadrado es la conocida fórmula, tantas veces memorizada,
pero quizás no siempre valorada en este aspecto del cálculo:"La
distancia entre 2 números cualquiera al cuadrado es la suma por la diferencia".
a² - b²
= (a + b) · (a - b)
Ejemplo:
9² = 81, 5² = 25, 81 - 25 = 56, es decir: (9 + 5) · (
9 - 5 ) = 14 x 4 = 56
Esto, obviamente, nos puede permitir
calcular números al cuadrado a partir de los que ya conocemos:
Ej. Cuánto será 26²,
si sabemos que 25² = 625 ?
Sólo tenemos que sumar 25 +
26 = 51, y esto, añadirlo al 625, o sea, 625 + 51 = 676
Ejercicio: Cuánto es 37²,
si sabemos que 30² = 900 ? >>>
Suma = 67, Diferencia = 7
Con un poco de habilidad calcularemos
67 x 7 = 469 y lo sumaremos a 900, para obtener: 37² = 1.369
EJERCICIO: Cuánto
es 54², si sabemos que 50² = 2.500 ?
Cuál será la diferencia entre 41² y 26²
?
- Un
método rápido de calcular números al cuadrado
-
-
a) Comenzaré con el
cuadrado
de los números de 2 cifras acabados en 5:
El
cuadrado de los números
tipo 15, 25, 35, etc. se puede hacer de manera muy rápida:"Multiplicando
la decena propia por la siguiente y añadiendo un 25 detrás"
-
Veamos ahora algunos ejemplos:
Ej. 15²: multiplicamos su decena 1
por la siguiente 2, y obtenemos 2
añadimos un 25 detrás y tenemos el 225, que es 15².
Ej. 45² : 4
x 5 = 20, añadimos el 25 y sale 2.025 = 45²
Ej. 65² : 6
x 7 = 42, añadimos el 25 y ya esta el 65² = 4.225
(¿sorprendente o no?)
-
-
b) Cuadrado de los números de
dos cifras acabados en 1:
El
cuadrado de los números
tipo 11, 21, 31, etc. se puede calcular de modo rápido en tres partes:"Cuadrado
de la decena, el doble de la decena, añadimos un 1"
-
Ejemplos: 11²: cuadrado de la decena 1 x 1 = 1
el doble de la decena 1 + 1 = 2
le añadimos un 1 >>>> y obtenemos el 121 = 11²
Ej. 31²: cuadrado
de la decena 9, el doble de la decena 6, le añadimos un 1
>>> 31² = 961 Si la suma
de las decenas pasa de 9, entonces nos llevamos 1 al construir el número:
-
Ej. 61²: cuadrado de la decena 36, el doble de la
decena 12 en este caso, al pasar de 9 la suma
nos llevamos 1, o sea, 372, y le añadimos un 1 >> 61²
= 3.721
-
-
c) Cuadrado de los números de
dos cifras acabados en 9:
El cuadrado de los números
tipo 19, 29, 39, etc. se puede calcular de manera rápida en tres
partes: "Al cuadrado de la decena siguiente
le añadimos el 0, restamos el doble de la decena siguiente y añadimos
un 1"
-
Ej. 29²: cuadrado de la
decena siguiente 3 x 3 = 9, añadimos el 0, o sea, 90
le restamos el doble de la decena 3 + 3 = 6, es decir, 90 - 6 = 84
le añadimos un 1 >>>> y obtenemos el 841 = 29²
Ej. 49²:
cuadrado de la decena siguiente 25 >> 250, restamos el doble de la decena
siguiente 10, 250 - 10 = 240, le añadimos un 1 >>> 49² = 2401
-
-
d) Cuadrado de los números de
dos cifras acabados en 2 (y de las demás cifras del 3 al 8):
De una manera similar a los acabados
en 1, haremos los acabados en 2: "Cuadrado de
la decena, el doble de la decena por 2, añadimos un 4 (cuadrado
del 2)"
-
Ej:
22²: cuadrado de la decena 2
x 2 = 4
el doble de la decena 2 + 2 = 4 por 2 = 8
le añadimos un 4 >>>> y obtenemos el 484 = 22²
Ej: 52²:
cuadrado de la decena 5 x 5 = 25
el doble de la decena 10 por 2 = 20, es decir, nos llevamos 2, por
tanto, 25+2 = 27 >> 270
le añadimos un 4 >>>> y obtenemos el 2704 = 52²
-
El método se puede generalizar
para los demás números.
-
Para acabar veamos los números
acabados en 3: "Cuadrado de la decena, el doble
de la decena por 3, añadimos un 9 (cuadrado del 3)"
-
Ej. 73²: cuadrado de la decena 7 x
7 = 49
el doble de la decena 7 + 7 = 14 por 3 = 42, nos llevamos 4, por
tanto, 49+4 = 53 >> 532
le añadimos un 9 >>>> y obtenemos el 5.329 = 73²
EJERCICIO: Calcular con este método los siguientes números
al cuadrado:
35² = ... ; 41² = ... ;
32² = ... ; 75² = ... ;
59² = ... ; 115² = ...
Método
de los "productos equidistantes"
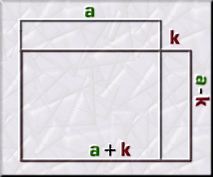Un aspecto interesante de los
números
al cuadrado es la "pérdida" que se produce si aumentamos y disminuimos
los números
en una cantidad constante, es decir, la diferencia de área entre
cuadrados y rectángulos con un mismo perímetro.
Tomamos un cuadrado de lado a y
lo convertimos en un rectángulo de lados: a
+
k y
a
-
k.
Veamos
lo que ocurre con un ejemplo numérico: 24²
= 576
>
25 x 23 = 575 (-1)
Hemos sumado y restado 1 y la distancia es 1²
>
26 x 22 = 572 (-4)
Hemos sumado y restado 2 y la distancia es 2²
>
27 x 21 = 567 (-9)
Hemos sumado y restado 3 y la distancia es 3²
>
28 x 20 = 560 (-16)
Hemos sumado y restado 4 y la distancia es 4²
> 29 x 19 = 551 (-25)
Hemos sumado y restado 5 y la distancia es 5²
Podemos concluir, por tanto, que:
"La diferencia
entre el área de un cuadrado y el área de un rectángulo,
generado a partir de aquel, es igual al cuadrado de la deformidad aplicada"
De aquí también se puede
sacar una aplicación numérica en el cálculo rápido
del producto de números que sean equidistantes a un número
al cuadrado, así, si observamos que 18 y 12 son equidistantes al
15, podremos calcular muy rápidamente 18 x 12, dado que 15²
= 225 y la distancia
es 3² = 9,
deducimos que 18 x 12 = 216.
Sólo
se puede aplicar cuando ambos factores son pares o ambos son impares.
Este "método de los productos equidistantes" es muy eficaz con la
sola condición de memorizar una buena serie de números al
cuadrado y de observar rápidamente si un producto lo permite o no.
EJERCICIO: Calcular con este método aquellos productos que permitan
su aplicación:
29 x 21 = ... ; 35 x 30 = ... ; 18 x 12 = ... ; 23 x 31 = ... ; 37 x 32
= ... ; 54 x 46 = ...
TRIÁNGULOS PITAGÓRICOS
ENTEROS
Expresiones matemáticas
para obtener triángulos rectángulos con valores enteros
-
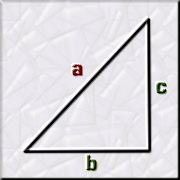El gran Pitágoras de Samos nos legó su archiconocido Teorema
de los triángulos rectángulos, pilar fundamental de cálculos
geométricos y trigonométricos, en el que se relacionan las
medidas de los catetos y de la hipotenusa: a²
= b² + c²
-
Dado que al aplicar esta fórmula matemática hemos de acabar
calculando una raíz cuadrada, casi siempre nos encontraremos que
no obtenemos valores exactos, o mejor dicho, valores enteros.
Al propio Pitágoras le debemos el triángulo rectángulo
arquetipo de medidas 3, 4 y 5, pero si lo que pretendemos
es utilizar otros triángulos rectángulos con valores enteros
casi nunca lo conseguiremos y acabaremos recurriendo a este triángulo
pitagórico (3, 4, 5) o a sus múltiplos.
Dedico esta sección a exponer unas expresiones matemáticas
que
nos permitirán obtener la mayoría de los triángulos
rectángulos de valores enteros que existen, son el fruto de una
buena idea inicial y de un estudio exhaustivo posterior. Así que
podéis tomar buena nota y, de este modo, tener una pequeña
herramienta con la que podréis generar problemas, etc. que tengan
por solución siempre valores enteros, o simplemente ver este capítulo
como una curiosidad matemática más.
-
La primera expresión nos genera las 3 medidas de triángulos
rectángulos en que el cateto pequeño es un número
impar:
2n
+ 1, 2n(n + 1),
2n²
+ 2n + 1
-
Así para n = 1 obtenemos los valores: 3,
4 y 5
(¿os
suena de algo?). Para n = 2: 5,
12,
13,
etc.
-
La segunda expresión nos genera las 3 medidas de triángulos
rectángulos en que el cateto pequeño es un número
par:
2(n
+ 1), n(n + 2),
n²
+ 2n + 2
-
Ej. para n = 1 obtenemos los valores: 4,
3
y 5 (otra
vez). Para n = 3: 8,
15,
17,
etc.
Veamos una tabla con los 7 primeros valores de cada una:
-
-
|
2n + 1
|
2n(n + 1) |
2n²
+ 2n + 1 |
n
|
2(n
+ 1) |
n(n
+ 2) |
n²
+ 2n + 2 |
|
3 |
4 |
5 |
1 |
4 |
3 |
5 |
|
5 |
12 |
13 |
2 |
6 |
8 |
10 |
|
7 |
24 |
25 |
3 |
8 |
15 |
17 |
|
9 |
40 |
41 |
4 |
10 |
24 |
26 |
|
11 |
60 |
61 |
5 |
12 |
35 |
37 |
|
13 |
84 |
85 |
6 |
14 |
48 |
50 |
|
15 |
112 |
113 |
7 |
16 |
63 |
65 |
-
A las dos expresiones expuestas
tendríamos que añadir una constante k, que al multiplicarla
por cada uno de los valores obtenidos y tomando diferentes valores nos
permita obtener los múltiplos de estas medidas, que obviamente,
también cumplen el Teorema de Pitágoras:
-
[2n
+ 1, 2n(n + 1), 2n²
+ 2n + 1] · k
[2(n
+ 1), n(n + 2), n²
+ 2n + 2] · k
-
Ahora ya tenéis un buen puñado de ejemplos y con las expresiones
matemáticas podréis obtener más.
De todas formas estos no son los únicos
y, por eso, acabé por buscar otro algoritmo de cálculo aún
más general.
Partiendo de la conocida regla, expuesta
en el capítulo anterior, que dice que:
-
"La distancia entre 2 números cualquiera al cuadrado es la
suma por la diferencia"
x² - y²
= (x + y) · (x - y)
-
Se puede hacer la siguiente demostración:
Si tenemos un número a, que es múltiplo de otros,
lo podremos expresar como a = x · y
Según
el Teorema de Pitágoras: a²=
c²
-
b²
= (c + b) · (c - b)
De aquí podemos deducir que: x² · y² =
(c + b) · (c - b), y por tanto:
x²
= c + b
y² = c - b Si
ahora resolvemos este sistema de ecuaciones tendremos que:
-
c
=
(x²
+ y²) / 2 , b =
(x² - y²) / 2
, a = x · y
-
O sea, que dado un cateto que mide a lo
podremos expresar en forma de producto de dos divisores: x · y (incluso
los números primos: a = a · 1 => x = a, y = 1, cumplen
esta fórmula => ver la tabla) y a partir de estos
hallamos que: el otro
cateto es la mitad de la diferencia de los cuadrados de sus divisores y su hipotenusa
es la mitad de la suma de los cuadrados de sus divisores.
-
El único pequeño problema que surge aquí es que al
tener que dividir por 2 en algunos casos (si un divisor es par y
el otro impar) no salen valores exactos, pero sus múltiplos pares
sí que lo serán y, en cualquier caso, como máximo
tendremos un decimal .5 igualmente muy interesante.
Veamos ahora unos cuantos ejemplos:
-
-
|
a = x · y |
b=
(x² - y²) / 2 |
c=
(x² + y²) / 2 |
a = x · y |
b=
(x² - y²) / 2 |
c=
(x² + y²) / 2 |
|
27 = 9 · 3 |
(9² - 3²) / 2 =
36 |
(9² + 3²) / 2 =
45 |
45 = 15 · 3 |
(15² - 3²) / 2 =108 |
(15² + 3²) / 2 =117 |
|
32 = 8 · 4 |
(8² - 4²) / 2 =
24 |
(8² + 4²) / 2 =
40 |
48 = 8 · 6 |
(8² - 6²) / 2 =
14 |
(8² + 6²) / 2 =
50 |
|
33 = 11 · 3 |
(11² - 3²) / 2 =
56 |
(11² + 3²) / 2 =
65 |
17 = 17 · 1 |
(17² - 1²) / 2 =144 |
(17² + 1²) / 2 =145 |
|
35 = 7 · 5 |
(7² - 5²) / 2 =
12 |
(7² + 5²) / 2 =
37 |
36 = 9 · 4 |
(9² - 4²) / 2 = 32.5 |
(9² + 4²) / 2 = 48.5 |
En este último ejemplo tenemos
que a =
36, b =
32.5, c =
48.5, de aquí podemos deducir que sus múltiplos
pares sí son enteros como: a =
72, b =
65, c =
97, a =
144, b =
130, c =
194, etc.
-
Hasta aquí este estudio, para
concluir sólo diré que todavía queda un grupo de triángulos
rectángulos de valores enteros que no se generan con ninguna de
las expresiones expuestas, pero sí que con ellas obtendremos la
mayoría de los que existen y, por tanto, me parecen de gran utilidad.
- Cálculo
de la diagonal de una figura geométrica que no existe!
-
- Si queremos calcular lo que mide la
diagonal de un cuadrado conociendo lo que miden sus lados, sólo
necesitaremos aplicar el Teorema de Pitágoras.
Así un cuadrado de lado 1,
tendrá una diagonal que mide V¯2¯
(raíz
cuadrada de 2)
A partir de aquí deduciremos
que la diagonal de un cuadrado de lado n mide: d
=n · V¯2¯
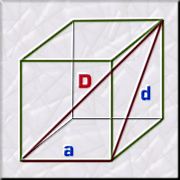
Si ahora queremos
calcular lo que mide la diagonal de un cubo, entre dos vértices
de caras opuestas, también podremos aplicar el Teorema de Pitágoras
si triangulamos el cubo y observamos el triángulo rectángulo
formado por una arista inferior a,
la diagonal de la cara lateral d
y la diagonal grande D.
Así observaremos
que D² =
a² + d²
En el caso del cubo de arista a = 1
la diagonal lateral d = V¯2¯
y, por tanto:D² =
1² + (V¯2¯)²
= 1 + 2 = 3 => D = V¯3¯
Obviamente podremos afirmar que la diagonal grande de un cubo de lado n
mide: D =n · V¯3¯
- Con
todo esto, y si seguimos este procedimiento de triangulación, podríamos
calcular cuanto miden las diagonales de figuras geométricas de más
de 3 dimensiones, es decir, de figuras que no existen, ni podemos tampoco
imaginar dada nuestra limitación tridimensional.
La diagonal
grande de una figura tipo cubo, pero de 4 dimensiones, será: D
= n · V¯4¯ = 2n
La diagonal grande de una figura tipo cubo, pero de 5 dimensiones, será: D
= n · V¯5¯, etc.
- ¡Qué
magnífico poder calcular algo que no podemos ni siquiera imaginar
su forma! ¡Me maravilla que una ciencia como las matemáticas
pueda llegar dónde no lo hace ni la imaginación!
Como me gustaría
llegar a un mundo cuatridimensional y pedir a sus habitantes que me mostrasen
un dado y observar este objeto en que su diagonal mide el doble que sus
aristas...
SOLUCIONES:
54² =
2.916 (2.500
+ 104 x 4 = 2.916)
41²
- 26² = (41 + 26) x (41 - 26) = 67 x 15 = 1.005
35² = 1.225
(3 x 4 = 12, 25)
41² = 1.681 (4²
= 16, 4 x 2 = 8, 1)
32² = 1.024 (3²
= 9, 3 x 2 x 2 = 12, 2² = 4) >> 9 +1 = 10, 2, 4 >> 1.024
75² = 5.625 (7
x 8 = 56, 25)
59² = 3.481 (6²
= 36, 6 x 2 = 12, 1) >> 360 - 12 = 348, 1 >> 3.481
115² = 13.225 (11 x 12 =
132, 25)
29 x 21 = 25² - 4² = 625 - 16 = 609
35 x 30 = 1.050 (no)
18 x 12 = 15² - 3² = 225 - 9 = 216
23 x 31 = 27² - 4² = 729 - 16 = 713
37 x 32 = 1.184 (no)
54 x 46 = 50² - 4² = 2.500 - 16 = 2.484
M.S. del 11 = { 209, 308, 407, 506, 605, 704,
803, 902, ...} (Distancia
clave 99, ...)
M.S. del 16 = { 448, 736, 2.176, 2.464, 2.752,
...}
(Distancia clave 288, ...)
M.S. del 17 = { 476, 629, 782, 935, 1.088,
1.394, ...} (Distancia
clave 153, ...)
Extracto de la página http://www.xtec.es/~bfiguera/curioso.html#quadrat
Autor: Blai Figueras Álvarez